哈希 Hash

Hash 就是 哈希。所有满足一个健（key）对应一个值（value）的形式的结构就是 hash，比如 HTTP 请求和 HTTP 响应的第二段。其实数组也是 hash，因为它也符合一个健一个值的定义。数组跟对象没有区别，数组就是对象。

哈希的应用

• 计数排序
• 基数排序
• 桶排序

计数排序

与之对应的比较排序，比较排序必须是两个数比较，它的过程中至少是遍历一次然后比较一次，最快的排序时间是 O(nlogn)。对应的排序快排，随机快排的时间复杂度就是 O(nlogn)。

原理：

1. 把数组的值（假设数组项有 0）作为 hash 的 key，hash 的 value 记录每个值出现了多少次。
2. 找出 hash 里面的最大值
3. 从 0 到 hash 最大值作为 v 轮询 hash， hash[v] 个 数组的值 push 到 新的数组
4. 返回新的数组

a <- {
  '0': 0,
  '1': 2,
  '2': 3,
  '4': 5,
  '5'：11,
  '6': 20,
  '7': 30,
  '9': 3,
  'length': 10 // JavaScript 里面数组的长度是 数组项的最大下标再加 1，所以是 10。
}
hash = {} // 定义一个 hash 记录 数组 a 的各项个数
index <- 0
while index < a['length']
	number = a[index]
	if hash[number] == undefined // hash 里面不存在 number，说明没记录 number
		hash[number] = 1 
	else
    hash[number] = hash[number] + 1
	end
  index <- index + 1
end
// 至此完成了 hash 记录数组 a 的各项及各项的个数
// 接下来轮询 hash，从数组 a 的最小值 到 最大值，这里简单设最小值 index2 为 0
index2 <- 0
max <- findMax(a)
newArr <- {} // 初始化一个新数组用于存最后排好序的数组
while index2 < max
	count = hash[index2]
	if count != undefined
		countIndex = 0
		while countIndex < count // 根据 hash 内记录的数组项的个数
			newArr.push(index2) // push 个数个数组项到新数组中
			countIndex <- countIndex + 1
		end
  end
  index2 <- index2 + 1
end
print newArr
end

得到计数排序的复杂度是 O(n+max)，比快排还快。

缺点

1. 必须要有个 hash 作为计数排序的工具，
2. 无法统计小数和负数进行排序

桶排序

多个桶，每个桶里面放多个数字，而且是一个范围内的数字。然后再对桶里面的数据进行排序。

比如：

hash = {
  1: [1, 2, 3, 5], // 1 - 10 内的数字，然后对这些数字排序
  2: [11],         // 10 - 20 内的数字
  3: [20],				 // 20 - 30 内的数字
  4: [30]					 // 30 - 40 内的数字
}

数组的项差异比较大时。相对于计数排序，桶排序节约空间但是浪费时间。桶的个数随意。

基数排序

十进制的基数是十，二进制基数是二。根据基数来排序的就叫基数排序。先按照个位进桶，出桶；然后按照十位进桶，再出桶；然后按照百位进桶，然后出桶。以此内推。

在这里看基数排序的可视化原理过程 https://visualgo.net/bn/sorting

桶的个数是固定的 十个。能适用很大很大的数字。

队列 Queue

队列的概念是先进先出。可以用数组实现，数组的 push 进队，数组的 shift 出队。

const queue = []
queue.push(1)
queue.push(2)
queue.push(3)
queue.shift() // 1 出队了
queue.shift() // 2 出队了

现实生活中的排队场景就是队列。

在基数排序出桶的时候就是用的队列。

栈 Stack

概念是先进后出。也可以用数组实现的，数组的 push 进队，数组的 pop 出队。

const queue = []
queue.push(1)
queue.push(2)
queue.push(3)
queue.pop() // 3 出栈了
queue.pop() // 2 出栈了

盗梦空间就是一个栈的场景。

链表 Linked List

因为数组是连续的，数组的缺点，要删除某个值时，还要把这个值后面的项目往前移。链表也是 hash

a1 <- {
  value: 0,
  next: a2
}
a2 <- {
  value: 2,
  next: a3
}
a3 <- {
  value: 3,
  next: undefined
}

改为 JavaScript 代码：

a1 = {
  value: 0,
  next: {
    value: 2,
    next: {
      value: 3,
      next: undefined
    }
  }
}

如果要删除 a2， 直接把 a1 的 next 改为 a3 就可以了，也就是 a2 没有人引用了。

删除 a2 的话，代码就是直接执行 a1.next = a3 就可以了。

a1 = {
  value: 0,
  next: {
    value: 3,
    next: undefined
  }
}

链表的缺点，如果要取链表的第 n 项，需要 a.next.next….next，a点 n - 1 个 next 才能得到；但是数组就很方便，arr[n - 1] 就能取到数组里面的第 n 项。

比较而已，就是链表删除快，数组查询快。

最上层的 a 是 head，链表的表头，也是节点，然后其他的点叫节点。

树

有层级结构的地方就有树，比如 DOM 树。

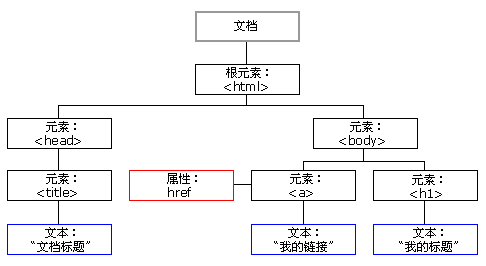
hash 分叉就是树，如果没有分叉就是链表。

节点下么有节点就是叶子节点，其他的叫普通节点，图上 DOM 树深度有 4 层，第 1/0 层 是 html，第 2 层是 head / body

二叉树

每次最多分 2 个叉，就是一个二叉树。

长满了叶子节点，满二叉树

左子树，右子树

二叉树的规律

完全二叉树，除了最后一层外，若其余层都是满的，并且最后一层是满的，或者最后一层的右边连续没叶子节点。

通过二叉树的规律可以用数组实现完全二叉树，满二叉树。在上表中可以表示二叉树的各项：arr = [1, 2,3, 4,5,6,7, 8,9,10,11,12,13,14,15, 16]。这里就很好查询二叉树上某个节点的值了，比如获取第 3 层的第 1 个节点，也就是 arr[2^2 - 1] 得到 4。

其他二叉树或者树的形式就不适用这种方法了，因为树中有空节点。

堆排序

所有节点都满足子节点小于或者大于父节点，那这个树就是一个堆。

大顶堆是最大元素出现在根节点。arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆是最小元素出现在根节点。arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

原理

1. 根据数组构建堆，将数组构建成一个无序的大顶堆（一般升序为大顶堆，降序为小顶堆）
2. 将堆顶元素与末尾元素交换，使末尾元素最大。然后继续调整堆为大顶堆，再将堆顶元素与末尾元素交换，使末尾元素为第二大元素。如此反复进行交换、调整、交换……。完成排序。

const heapSort = arr => {
  const adjuestHeap = (arr, i, arrLen) {
    const tmp = arr[i]
    for (let j = i*2 + 1; j < arrLen; j = j*2 + 1) {
      if (j + 1 < arrLen && arr[j] < arr[j + 1]) {
        j++
      }
      if (arr[j] > tmp) {
        arr[i] = arr[j]
        i = j
      } else {
        break
      }
    }
    arr[i] = tmp
  }
  
  const arrLen = arr.length
  
  for (let i = arrLen / 2 - 1; i >= 0; i--) {
    adjuestHeap(arr, i, arrLen)
  }
  
  for (let k = arrLen - 1; k > 0; k--) {
    const tmp = arr[0]
    arr[0] = arr[k]
    arr[k] = tmp
    adjuestHeap(arr, 0, j)
  }
}

参考链接

图解排序算法(三)之堆排序