为什么 0.1 + 0.2 === 0.30000000000000004
双精度浮点数的概念
双精度浮点数是JavaScript 的数值使用的数值形式,又称 64 位浮点数,由 IEE 754 (电气和电子工程师协会)制定的标准。
64 位浮点数的二进制位是由三个部分组成:
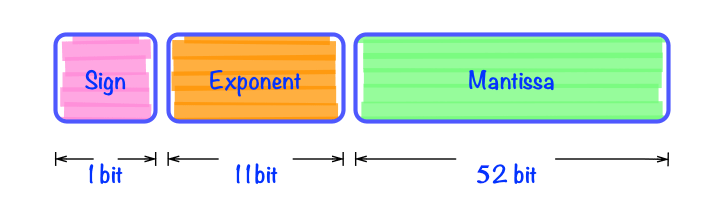
从左到右:
- 第 1 位 为 Sign 位,即符号位,表示浮点数是否是负数,所以说 1 就表示浮点数是负数,0 则表示是正数
- 从第 2 位到到 12 位,共 11 位,是指数部分。
类似于科学计数法中的M*10^N中的 N,只是这里的 10 替换成了 2 。
这部分中以2^10-1即1023,也即 1111111111代表 2^0,转换时需要根据 1023 作偏移调整。 - 从第 13 位到第 64 位,共 52 位,是小数部分,是浮点数具体数值的实际表示。
浮点数转换到二进制
第一步:改写整数部分
以 5.2为例。先不考虑指数部分,单纯的将十进制转换成二进制。整数部分很简单,十进制 5 转换成二进制为 101。
第二步:改写小数部分
0.2 的二进制转换,数值乘以 2,如果乘法计算的结果(> = 1.0)也就是有整数部分,则该位的值为 1,然后将剩余的小数部分用于下一次计算。直到结果为 1.0,转换结束。
| 位置 | 计算 | 结果 | 整数 | 位值 |
|---|---|---|---|---|
| 1 | .2 x 2 | .4 | no | 0 |
| 2 | .4 x 2 | .8 | no | 0 |
| 3 | .8 x 2 | 1.6 | yes | 1 |
| 4 | .6 x 2 | 1.2 | yes | 1 |
| 5 同第 1 位 | .2 x 2 | .4 | no | 0 |
| 6 同第 2 位 | .4 x 2 | .8 | no | 0 |
| 7 同第 3 位 | .8 x 2 | 1.6 | yes | 1 |
| 8 同第 4 位 | .6 x 2 | 1.2 | yes | 1 |
| 9 同第 1 位 | .2 x 2 | .4 | no | 0 |
| 10 同第 2 位 | .4 x 2 | .8 | no | 0 |
| 11 同第 3 位 | .8 x 2 | 1.6 | yes | 1 |
| 12 同第 4 位 | .6 x 2 | 1.2 | yes | 1 |
| … |
可以看出 0.2 的二进制值无法达到结果为 1.0 的情况,而是 .4,.8,1.6,1.2 一直循环,也就是二进制位值 0011 四位无限循环。二进制表示为:0.001100110011....
第三步:规格化
现在我们有了这么一串二进制 101.0011001100110011....。然后我们要将它规格化,也叫 Normalize。
其实原理很简单就是包装小数点前只有一个 bit。
于是我们就得到了一下表示:1.0100110011001100110011*2^2。到此我们已经把改写工作完成,接下来要把 bit 填充到三个组成部分中去了。
第四步:填充
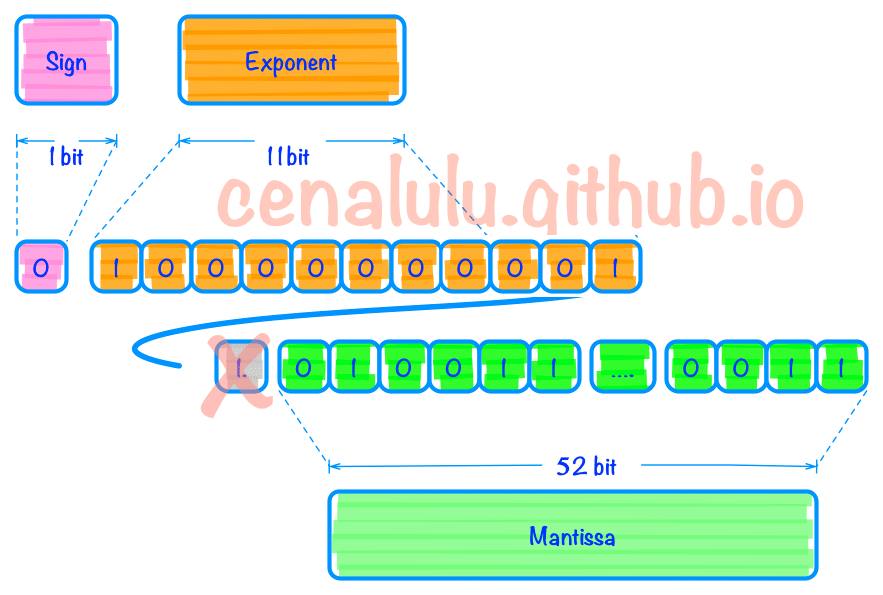
指数部分 Exponent:需要以 1023 作为偏移量调整。因此 2 的 2 次方,指数部分偏移成 2 + 1023 即 1025,表示成10000000001填入。
尾数部分 Mantissa:除了简单的填入外,需要特别解释的地方是 1.010011 中的整数部分 1 在填充时被舍去了。因为规格化后的数值整数部分总为 1。对于任何科学记数法,小数点始终移动到最左侧位置,以便没有前导零。例如,0.234 x 102 或 0.365 x 105。这些数字将写成 2.34 x 101 和 3.65 x 104。同样的规则用于二进制科学记数法,这意味着任何标准化的科学二进制数都以 1 开头。既然确认知道是 1,所以为了节省空间,这一位的 1 就被省略了。
具体填充后的结果见下图:
为什么 0.1 + 0.2 === 0.30000000000000004
现在我们按照上面的分析来分析下 0.1 + 0.2 为什么等于 0.30000000000000004
0.1 转换为二进制
| 计算次数 | 计算 | 结果 | 整数 | 位值 |
|---|---|---|---|---|
| 1 | .1 x 2 | .2 | no | 0 |
| 2 | .2 x 2 | .4 | no | 0 |
| 3 | .4 x 2 | .8 | no | 0 |
| 4 | .8 x 2 | 1.6 | yes | 1 |
| 5 | .6 x 2 | 1.2 | yes | 1 |
| 6 同第 2 位 | .2 x 2 | .4 | no | 0 |
| 7 同第 3 位 | .4 x 2 | .8 | no | 0 |
| 8 同第 4 位 | .8 x 2 | 1.6 | yes | 1 |
| 9 同第 5 位 | .6 x 2 | 1.2 | yes | 1 |
| 10 同第 2 位 | .2 x 2 | .4 | no | 0 |
| 11 同第 3 位 | .4 x 2 | .8 | no | 0 |
| 12 同第 4 位 | .8 x 2 | 1.6 | yes | 1 |
| 13 同第 5 位 | .6 x 2 | 1.2 | yes | 1 |
| … |
可以看出 0.1 的二进制值也是无法达到结果为 1.0 的情况的,而是 .4,.8,1.6,1.2 一直循环,也就是二进制位值 0011 四位无限循环。二进制表示为:0.0001100110011….
0.1 二进制规格化:
- 符号位
- 不是负数 所以符号位为 0
- 指数位
- 科学计数法,浮点数的小数点往后移动 4 位,表示为 1.100110011….x2^-4,方便计算计数部分就不再规格化为二进制。
- 尾数位
- 无限循环的最大值为 64 位浮点数制定的最大尾数位 52 位,所以表示为1001100110011001100110011001100110011001100110011010
方便后续计算表示为:
0.1 = 1.1001100110011001100110011001100110011001100110011010 x 2^-4
0.2 转换为二进制
从上面的案例我们已经得到了 0.2 的二进制数为:.001100110011….
0.2 二进制规格化
- 符号位
- 不是负数,所以是 0
- 指数位
- .001100110011…. 小数点往后挪 3 位,表示为 1.100110011….x2^-3,方便计算计数部分就不再规格化为二进制。
- 尾数位
- 同 0.1 的尾数,0.2 的尾数也是 1001100110011001100110011001100110011001100110011010
方便后续计算表示为:
0.2 = 1.1001100110011001100110011001100110011001100110011010 x 2^-3
0.1 的 64 位二进制 + 0.2 的 64 位二进制
0.1 = 2^-3 * 0.1100110011001100110011001100110011001100110011001101(0) |
即
sum = 2^-2 * 1.0011001100110011001100110011001100110011001100110011(1) |
sum 转换为十进制为 0.3000000000004
解决办法
转换为整数计算,计算完后返回小数点的位置
0.1 + 0.2 转换为 1 + 2 等于 3,再转换为小数 0.3
const plus = (num1, num2) => { |
参考链接
你应该知道的浮点数基础知识
译文:二进制数与浮点数的转换
JS魔法堂:彻底理解0.1 + 0.2 === 0.30000000000000004的背后
Is floating point math broken?
http://0.30000000000000004.com/
JavaScript 浮点数陷阱及解法