原文：Binary numbers – floating point conversion
作者：Thomas N

8位（1字节）的二进制数可以表示 0 到 255 范围内的十进制值，但是，这只包括整数而没有实数（例如分数），如 0.5 或 20.456 等。

十进制 181 的二进制形式

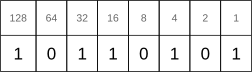
为了以二进制形式表示所有实数，需要更多位和明确定义的格式。所以就出现了浮点数。但是，浮点数只是接近实数而已。想象一下PI 3.14159265的数字……它永远不会结束。它需要无限多的位来表示这个数字。二进制浮点数只是精度和范围之间的折中的办法。根据用途，有不同大小的二进制浮点数。

为什么称它为“浮点数”？

顾名思义，点（小数点）可以浮动。浮点数的格式是使用科学计数法。科学计数法是一种书写数字的形式，当数字太大或太小，不能以十进制形式方便地写时，就用科学计数法。基数为 10 科学记数法是 x x 10y，允许小数点移动。

例如，数字523.0可以用科学记数法写成 523.0 x 10⁰，52.30 x 10¹ 或 5.230 x 10²。“浮动”小数点出现在数字 x 中的不同位置取决于指数 y。将小数点向右移动一个位置会增加指数，向左移动指数会减小指数。

二进制浮点数

两种最常见的浮点存储格式由IEEE 754标准（电气和电子工程师协会，一个定义标准的大型组织）定义：

• 32位浮点数（也称为单精度浮点数）
  • 1位符号位，8位指数位，23位尾数位
• 64位浮点数（也称双精度浮点数）
  • 1位符号位，11位指数位，52位尾数位

下图显示了二进制形式的32位浮点数。高亮的部分指示出符号位“S”，指数 Exponet 和 尾数 Mantissa 的三部分的位置：

32位浮点数：灰色表示的位的位置和各个位置位的值全部设置为 1

以下是浮点数的示例，其科学记数法为 + 34.890625 x 10⁴。符号位是加号。尾数是 34.890625，指数是 4。因为我们在十进制系统中，所以基数是10。

有关位区域的更多信息：

• 符号位

  • 一个单一的位。符号位表示数字是否为负数。因此，1 表示该数字是负数，0 表示该数字是正数。

• 尾数位

  • 23位（单精度浮点）可以表示 8388608 个不同的值。有时也称为有效数字。

• 指数位

  • 8位（单精度浮点）可以表示 256 个不同的值。
    

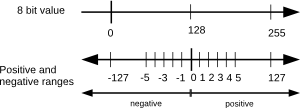
    具有负和正范围的8位值的图

    允许正指数和负指数，范围的一半（0 - 127）用于负指数，另一半（128 - 255）用于正指数。正指数 10⁵ 的值为 5 + 127 = 132，而负指数 10^-8 的值为 -8 + 127 = 119。

将十进制浮点数转换为二进制

将十进制值转换为二进制值需要在其中添加每个位位置值

从图中可以得出二进制数 10110101 的十进制值为 1 + 4 + 16 + 32 + 128 = 181

处理浮点数时，过程非常相似，但还需要一些额外的步骤。将十进制浮点数转换为二进制形式比使用其他方式更复杂。首先解释转换为二进制，因为它逐步显示和解释二进制浮点数的所有部分。

浮点数具有整数部分和小数部分。例如，在数字 34.890625，整数部分是小数点前面的数字（34），小数部分是小数点后面的其余部分（.890625）。以下是将十进制数转换为二进制数的步骤（以下将详细说明这些步骤）：

1. 将十进制数转换为二进制科学记数法，独立处理积分和小数部分
2. 然后将科学二进制数归一化（小数点移动到最左侧位置，相应地调整指数）
3. 指数转换为二进制
4. 二进制浮点数由所有转换的数字部分构成。尾数的前 1 个被省略

步骤一

第一步是将数字转换为二进制科学记数法。要将此浮点值转换为二进制，首先独立处理整数和小数部分。

将整分部分转换为二进制：

整数部分转换：34 的二进制数是 10 0010。
首先整数部分除以 2（2 因为我们想要转换为二进制）。然后结果的整数部分再次用 2 除以，依此类推，直到整数部分为 0。

计算	结果	整数部分	余数（位）
34 / 2	17	17	0
17 / 2	8.5	8	1
8 / 2	4	4	0
4 / 2	2	2	0
2 / 2	1	1	0
1 / 2	0.5	0	1

结果是以相反的顺序计算。从下到上读取二进制数为 10 0010（提示：以 4 个为一组写入二进制数，这是一个字节，使其更容易阅读）。

将小数部分转换为二进制：

转换小数部分，不是用整数部分的除法，而是用乘法。如果乘法计算的结果（> = 1.0）也就是整数，则该位为 1。然后将剩余的小数部分用于下一次计算。直到结果为 1.0，转换结束。但是，有许多数字不会以 1.0 的结果结束。由于尾数有 23 个可能的位（在单个精度浮点数中），一旦达到 23 位，转换就会结束。还是以小数部分 .890625 为例，我们来进行转换计算：

计算	结果	整数 ( > = 1 )	位
.890625 x 2	1.78125	yes	1
.78125 x 2	1.5625	yes	1
.5625 x 2	1.125	yes	1
.125 x 2	0.25	no	0
.25 x 2	0.5	no	0
.5 x 2	1	yes	1

结果位按照它们的写入顺序计算，这给出了二进制数 11 1001。数字 34.890625 组合的整数和小数部分给出了基数 2 的科学二进制数 100010.111001 x 2⁰（34 = 10 0010 和 .890625 = 11 1001），因为它是二进制数（而不是基数为 10 的十进制数）。

步骤二

归一化科学数字意味着通过相应地调整指数将小数点移动到最左边的位置。对于数字 100010.111001 x 2⁰，小数点可以向左移动 5 个位置，这使指数增加 5：1.00010111001 x 2⁵。

注意：对于任何科学记数法，小数点始终移动到最左侧位置，以便没有前导零。例如，0.234 x 10² 或 0.365 x 10⁵。这些数字将写成 2.34 x 10¹ 和 3.65 x 10⁴。同样的规则用于二进制科学记数法，这意味着任何标准化的科学二进制数都以 1 开头。

步骤三

二进制数的归一化导致调整的指数为 5。如前所述，二进制浮点指数具有负范围和正范围。因此，必须将 127 添加到指数 5，然后转换为二进制：5 + 127 = 132，其为二进制的 1000 0100。所以指数部分的值为 1000 0100。

步骤四

现在，可以构造二进制浮点数。合并步骤一到步骤三的结果：

• 二进制形式的正数：1.00010111001
• 二进制形式的指数：1000 0100

现在可以将这些数字填充到32位浮点数的位区域中。

• 符号位
  • 数字为正数，表示符号为0
• 尾数位
  • 尾数是 00010111001。前面的1去了哪里？如步骤二中所述，任何科学记数都以前面的 1 结束。因此，前面的 1 被省略，因为对于状态已知的位，不必浪费空间。
• 指数位
  • 指数是1000 0100

所以 34.890625 的浮点数值为0 10000100 0001011100100000000000：

转换的尾数值是“左对齐”，这意味着数字右侧的任何未使用的位都用 0 填充以达到二进制数的大小。双精度64位二进制数将具有更多可用位，如果需要可以提供更好的精度。转换的指数是“右对齐”，并且数字左侧的任何未使用的位都用0填充。

将二进制浮点数转换为十进制数

将二进制浮点数转换为十进制比十进制转二进制浮点数要简单得多。为简单起见，我们将再次使用先前转换的数字并将其转换回十进制数。如果一切正常，结果应该是 34.890625。

二进制 32 位浮点数为：0 10000100 0001011100100000000000

同样，这是一个正数（第一位，符号，为0），指数为10000100，尾数为1.00010111001（在末尾省略任意零，并在小数点前面加上省略的1）。

将指数转换为十进制：

转换是基本二进制到十进制转换。

2² + 2⁷ = 132
or 4 + 128 =132

由于指数的正负范围为 + - 127（如前所述），因此必须从转换后的值中减去 127： 132 - 127 = 5

得到的指数是5。

整个尾数现在可以转换为十进制：

转换尾数不需要撤消规范化。整数可以计算如下： 1.00010111001 x 2⁵

负指数：（2⁰ + 2^-4 + 2^-6 + 2^-7 + 2^-8 + 2^-11）x 2⁵ = 34.890625 或分数：（1 + 1/16 + 1/64 + 1/128 + 1/256 + 1/2048）x 25 = 34.890625

该数字现在已成功转换为十进制，结果为 34.890625，这是我们开始使用的浮点数的十进制表示。