按位运算
概述
按位运算是把操作数当作 32 位的 bit 序列(0 和 1 组成的序列),而不是十进制、十六进制或者八进制数值。返回标准的 JavaScript 数值。
| 运算符 | 用法 | 描述 |
|---|---|---|
| 按位与 | a & b | a,b 都是 1 时,返回 1 否则 0 |
| 按位或 | a | b | a 或者 b 是 1 时,返回 1 否则 0 |
| 按位异或 | a ^ b | a 和 b 有且只有一个是 1,返回 1 否则 0 |
| 按位非 | ~a | 反转 a,如果 a 是 0 返回 1, 如果 a 是 1 则返回 0 |
| 左移 | a << b | a 向左移动 b 位,右边用 0 填充,b < 32 |
| 有符号右移 | a >> b | a 向右移动 b 位,丢弃被移出的位,b < 32 |
| 无符号右移 | a >>> b | a 向右移动 b 位,丢弃被移出的位,并使用 0 在左侧填充,b < 32 |
1010 & 1011 // 1010 |
计算机中存储的有符号 32 位整数
所有的按位操作数都会被转成补码形式的有符号 32 位整数。
- 原码表示法是在数值前面增加一位符号位,正数是 0,负数是 1。比如 十进制 3 的 8 位二进制表示为 0000 0011,而 -3 表示为 1000 0011。
- 反码表示法,正数的反码就是自身;负数的反码是在原码上,符号位不变,其他位各位取反。-3 的反码是 1111 1100
- 补码表示法,正数的补码就是自身;负数的补码是在反码上,符号位不变,加 1。-3 的补码是 1111 1101。
可以看出补码保证了当一个数是正数时,最左边的比特位是 0,当是一个负数时,最左边的比特位是 1。最左边的比特位被称为符号位。
原码容易被人脑直接识别并用于计算,但是对与计算机来说并不友好。所以计算机系统中,数值一律用补码来表示、运算和存储。使用补码,可以将符号位和数值域同意处理,将加法和减法统一处理。
按位运算
计算机中存储数字都是补码形式,运算也是用的补码,得到的结果也是补码
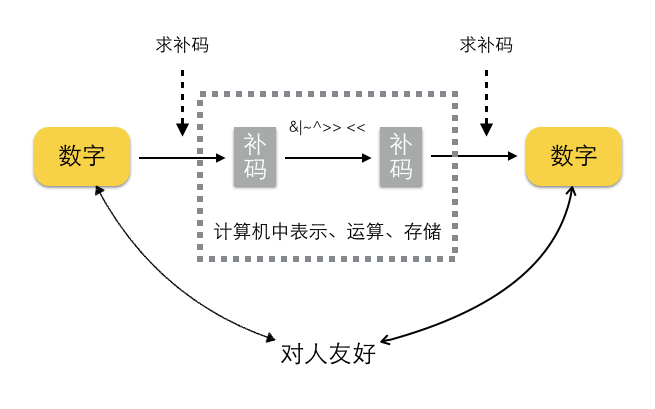
开发中的使用场景
交换两个数
原理是用位运算的异或运算
- 0^a = a
- a^a = 0
- a^b^c = (a^b)^c = a^(b^c)
const swap = (num1, num2) => { |
如果 num1 和 num2 值一样时候,num1 ^ num2 的值是 0,这个时候就不能用这种方案互换了。