FE NOTEBOOK 🚀

什么是结构化编程

一种编程范式。它采用子程序、代码区块、for 循环以及 while 循环等结构来取代 goto 指令的程序。

特点

仅有一个入口
仅有一个出口
结构中任一部分都应有执行到的机会
不出现死循环

结构化编程描述算法的方法：伪代码，流程图。

以下写画下常见的九大排序算法的伪代码和流程图，还有 JavaScript 的实现。

冒泡排序

两两比较，大的往后排。第 1 项与第 2 项，大的往后；然后第 2 项与第 3 项比较，大的往后；然后第 3 项与第 4 项比较，大的往后排；然后第 4 项与第 5 项比较，大的往后排；…直到第 n 项完成一轮排序。

进行下一轮排序时，可以确定前一轮已经确定了数组后面的轮数的项已经排好了，就不需要再进行排序。

…… 以此类推完成 n - 1 轮排序

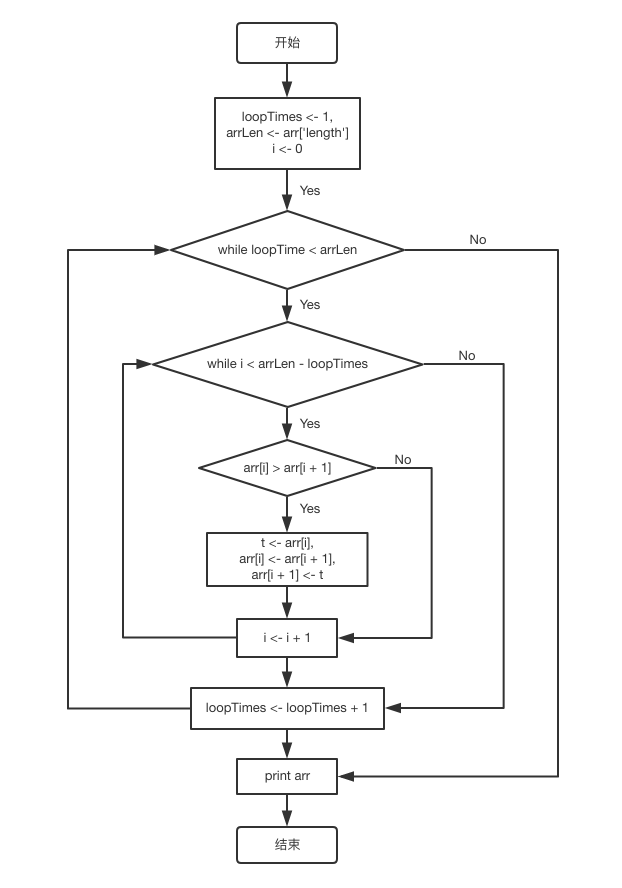
流程图

1271540189276_.pic.jpg

伪代码

if !arr || !arr.length
  print arr
end
loopTimes <- 1
arrLen <- arr['length']
i <- 0
while loopTimes < arrLen
  // arrLen - loopTimes 是每一次循环都能确定一个当前循环的最大值，
  // 下次再循环的时候，可以减少一次循环
  while i < arrLen - loopTimes
    if arr[i] > arr[i + 1]
      t <- arr[i]
      arr[i] <- arr[i + 1]
      arr[i + 1] <- arr[i]
      i <- i + 1
    else
      i <- i + 1
    end
    loopTimes <- loopTimes + 1
  end
end
print arr

JavaScript 实现

const bubbleSort = arr => {
  if (!arr || !arr.length) {
    return arr
  }
  const arrLen = arr.length
  for (let loopTimes = 1; loopTimes < arrLen; loopTimes++) {
    for (let i = 0; i < arrLen - loopTimes; i++) {
      if (arr[i] > arr[i + 1]) {
          [arr[i], arr[i + 1]] = [arr[i + 1], arr[i]]
      }
    }
  }
  return arr
}

如果 loopTimes 等于 1 的循环完成后，数据并没有交换，那么就可以确定数组是有序的，不需要再进行之前的比较了，可以定义一个变量 swapFlag，标记是否发生交换，如果没有交换就直接退出程序。

JavaScript 优化实现

const bubbleSort = arr => {
  if (!arr || !arr.length) {
    return arr
  }
  const arrLen = arr.length
  let swapFlag = false
  for (let loopTimes = 1; loopTimes < arrLen; loopTimes++) {
    for (let i = 0; i < arrLen - loopTimes; i++) {
      if (arr[i] > arr[i + 1]) {
        [arr[i], arr[i + 1]] = [arr[i + 1], arr[i]]
        swapFlag = true
      }
    }
    if (swapFlag == false) {
      break;
    }
  }
  return arr
}

效率测试

随机生成一个长度为 100，最大值为 1000 的超大数组排序，通过 console.time 记录排序时间

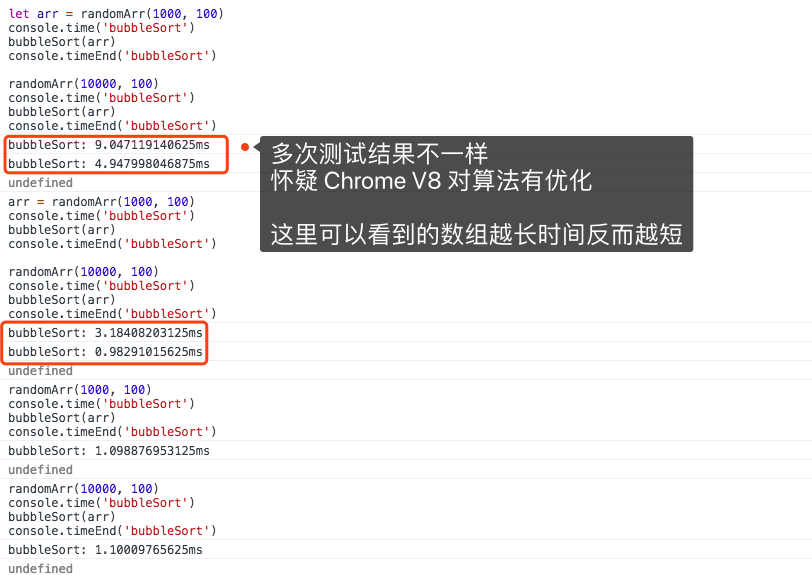
const randomArr = (arrLen = 100, maxValue = 1000) => {
  let arr = []
  for (let i = 0; i < arrLen; i++) {
    arr[i] = Math.floor((maxValue + 1) * Math.random())
  }
  return arr
}

let arr = randomArr(1000, 100)
console.time('bubbleSort')
bubbleSort(arr)
console.timeEnd('bubbleSort')
// bubbleSort: 4.602783203125ms

randomArr(10000, 100)
console.time('bubbleSort')
bubbleSort(arr)
console.timeEnd('bubbleSort')
// bubbleSort: 308.89599609375ms

看起来数组长度增加 10 倍，排序时间增加差不多 100 倍。多次在 Chrome 上测试，却发现每次运行的时间不同，而且还出现了数组越长时间越短的情况。不知道是不是 V8 进行了优化。

1301540267403_.pic_hd.jpg

复杂度

第一轮循环执行是 n - 1
第二轮 n - 2
第三轮 n - 3
…
第 n 轮 n - n

得出 (n - 1) + (n - 2) + (n - 3)+…1 等差数列求和，即 n*(1 + (n -1)) /2。解开得到 n ^ 2 / 2，所以时间复杂度为 O(n^2)。

选择排序

循环选择出数组中的最大值，将最大值挪到数组最后；再进行下一次循环，选择出第二大的项…… 以此类推完成排序。或者循环选择出数组中的最小值，将最小值挪到数组最前面；再进行下一次循环，选择出第二小的项…… 以此类推完成排序。

伪代码

if !arr || !arr.length
  print arr
end
loopTimes <- 1
arrLen = arr['length']
while loopTimes < arrLen
  maxPos <- 0
  j <- 1
  lastIndex <- arrLen - loopTimes
  while j <= lastIndex
    if arr[j] > arr[maxPos]
      maxPos <- j
      j <- j + 1
    else
      j <- j + 1
    end
  end
  if maxPos != lastIndex
    t <- arr[lastIndex]
    arr[lastIndex] <- arr[maxPos]
    arr[maxPos] <- t
    loopTimes <- loopTimes + 1
  else
    loopTimes <- loopTimes + 1
  end
print arr
end

JavaScript 实现

const sectionSort = arr => {
  if (!arr || !arr.length) {
        return arr
    }
    const arrLen = arr.length;
    for (let loopTimes = 1; loopTimes < arrLen; loopTimes++) {
        let maxPos = 0,
            lastIndex = arrLen - loopTimes;
        for (let j = 1; j <= lastIndex; j++) {
            if (arr[j] > arr[maxPos]) {
                maxPos = j
            }
        }
        if (maxPos != lastIndex) {
            [arr[lastIndex], arr[maxPos]] = [arr[maxPos], arr[lastIndex]]
        }
    }
    return arr
}

在每次循环获取最大值时，同时可以获取到最小值，可以通过这个来优化一下算法。

优化实现

const sectionSort = arr => {
  let begin = 0,
      end = arr.length - 1;

  while (begin < end) {
    let maxPos = begin,
        minPos = begin;

    for (var i = begin; i < end; i++) {
      if (arr[i] > arr[maxPos]) {
        maxPos = i
      }
      if (arr[i] < arr[minPos]) {
        minPos = i
      }
    }

    [arr[end], arr[maxPos]] = [arr[maxPos], arr[end]]

    if (minPos == end) {
      minPos = maxPos
    }

    [arr[begin], arr[minPos]] = [arr[minPos], arr[begin]]

    begin++
    end--
  }
  return arr
}

插入排序

类比扑克牌时，拿到牌后的整理牌的操作。第 2 个和第 1 个比较大小，排好序；第 3 个和前面两个比较，排好序；第 4 个和前面三个比较，排好序；以此类推。和前面已经排好序的元素序列中从后向前扫描。

伪代码

index <- 1
arrLen <- arr.length
while index <= arrLen - 1
  last <- index
  tmp <- arr[last]
  while last > 0 && tmp < arr[last-1]
    arr[last] <- arr[last-1]
    last <- last - 1
  end
  arr[last] <- tmp
  index <- index + 1
end
print arr

JavaScript 实现

const insertionSort = arr => {
  for (let i = 1; i < arr.length; i++) {
    const tmp = arr[i];
    for (var j = i; j > 0 && arr[j - 1] > tmp; j--) {
      arr[j] = arr[j - 1]
    }
    arr[j] = tmp
  }
  return arr
}

splice 方法实现插入排序

const insertionSort = arr => {
  for (let i = 1; i < arr.length; i++) {
    for (let j = 0; j < i; j++) {
      if (arr[i] < arr[j]) {
        arr.splice(j, 0, arr[i])
        arr.splice(i + 1, 1)
        break
      }
    }
  }
  return arr
}

参考链接

伪·从零开始学算法 - 1.4 结构化编程与逻辑结构
 九种常见排序的比较和实现
 排序算法

n 方排序：冒泡、选择、插入排序

什么是结构化编程

特点

冒泡排序

复杂度

选择排序

插入排序

splice 方法实现插入排序

参考链接